Hooke's Law (Edexcel A Level Further Maths: Further Mechanics 1)

What is Hooke's Law?

• Up to now, strings have been modelled as inextensible
  • they cannot stretch (inelastic)
  • we assume that the tension measured at any point along the string is the same constant value
• Things that stretch (or compress, e.g. springs) are called elastic 
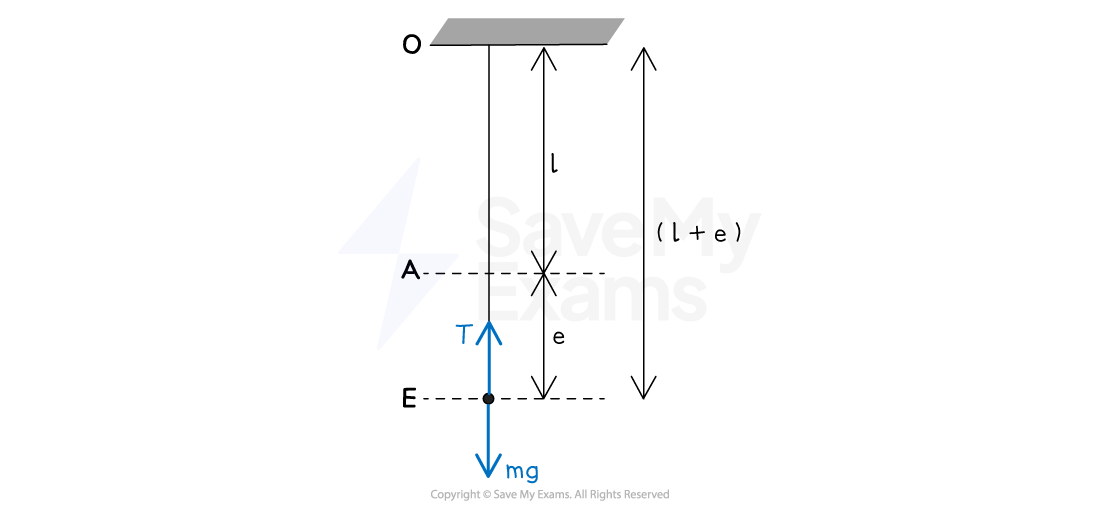
• Imagine two elastic strings held taut and at rest, but with one stretched further than the other
  • measuring the tension at different points along one string gives the same value,
  • but that "value" will be higher for the more stretched string than for the less stretched string
• Hooke's Law tells us that the value of tension, N, depends on how far it's been stretched (the extension, metres) beyond its natural (unstretched) length ( metres)
  • The law is 
  • where  is the modulus of elasticity, with units of Newtons,
    • it measures the stiffness of the material the string (or spring) is made from,
    • the higher  is, the stiffer the string / spring is
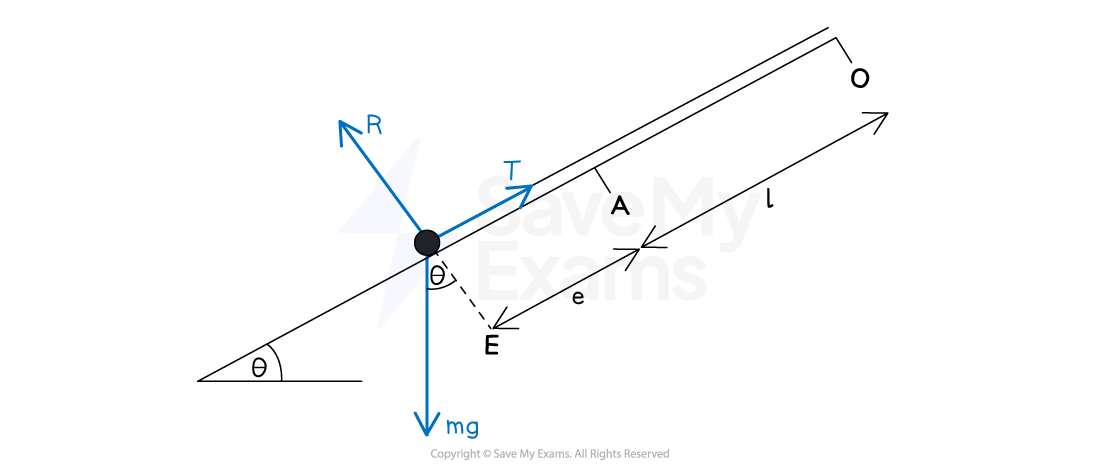
• Springs can be compressed but elastic strings can't (they'd go slack)
  • Hooke's Law works for compression of springs too
  • Instead of measuring extension, measures the length of compression (from its natural length)
    • just make sure any tension arrows reverse direction to be compression (thrust) arrows!

How do I use Hooke's Law for particles at rest under gravity?

• Imagine a particle of mass kg attached to the end of a light elastic string of natural length  metres, with modulus of elasticity N
• The other end of the string is attached to a ceiling at the point O and the particle hangs at rest at the point E, vertically beneath O
• The total length of the string, OE, will be greater than its natural length, OA (where A is  metres from O)
  • The weight of the particle has stretched the string downwards and the system is now in equilibrium
  • The equilibrium extension is often labelled as metres
    • The total length is therefore metres

• Two equations can be formed and solved simultaneously to find 
  • Applying Newton's 2nd Law (F=ma) upwards at E gives the first equation:
    • 
    • You could also resolve downwards giving the same relationship
  • Applying Hooke's Law gives the second equation:
    • 

How do I use Hooke's Law for particles resting on a smooth inclined plane?

• Imagine a particle of mass kg attached to the end of a light elastic string of natural length  metres, with modulus of elasticity N
• The other end of the string is attached to the top of a smooth inclined plane at the point O and the particle lies at rest at the point E on the slope
  • The equilibrium extension is metres
  • The angle of inclination of the plane is

• Again, two equations can be formed, which can be solved simultaneously to find 
  • Newton's 2nd Law up the slope at E gives the first equation:
    • 
  • Hooke's Law gives the second equation:
    • 
• Compression questions can have a spring attached to the bottom of the inclined plane
  • In this case, it rests on the slope at the point E, less than its natural length metres from the bottom
  • Use to measure the equilibrium compression
  •  now goes up the slope (thrust)

What if the particle rests on a rough inclined plane?

• A rough slope has a range of points on it at which the particle would remain in equilibrium
• With the setup above, the furthest possible equilibrium position from O is on the slope where the string has extended so much that the particle is on the point of sliding back up the slope
  • This still counts as equilibrium (as it's not actually moved yet)
  • Friction has reached its limiting value, (as it's on the point of moving)
  • Friction acts down the slope (stopping it from actually sliding up)

• Provided the string doesn't go slack (an extension of zero), a shortest possible equilibrium position from O exists on the slope where the string is extended only a small amount from its natural length and the particle is on the point of sliding down the slope
  • Again, this counts as equilibrium and friction reaches its limiting value
  • Friction now acts up the slope (stopping it from actually sliding down)

• In either case, four equations can be solved to find 
  • The first is from Newton's 2nd Law parallel to the slope
    • being careful to draw friction in the correct direction 
    • 
  • The second is from Newton's 2nd Law perpendicular to the slope
    • This gives you the reaction 
    • 
  • The third is from Hooke's Law
    • 
  • The fourth is from friction reaching it's limiting value
    • 
• If the particle is in equilibrium at a point between the two extremes above, friction is no longer "limiting"
  • You cannot use  (as )
• If, instead, the string is replaced by a spring, springs can't go slack so its shortest equilibrium position from O may, in fact, be when it's under compression
  
  • i.e. when the particle is less than the natural length, , from O

How do I find acceleration using Hooke's Law?

• You must first understand Hooke's Law in equilibrium before looking at moving (dynamical) particles
• Imagine a particle of mass kg attached to the end of a light elastic string of natural length  metres, with modulus of elasticity N
• The other end of the string is attached to a ceiling at the point O and the particle hangs at rest at the point E, vertically beneath O
  • The total length of the string is  metres, where  is the equilibrium extension
  • It helps to use as the equilibrium tension (to avoid confusing it with a different tension, , below)
  • can be found by drawing a force diagram in equilibrium and solving two equations
    • Newton's 2nd Law, 
    • Hooke's Law, 
• Now imagine pulling the particle down to the point B with extension where , under tension N, then letting go 
  • the particle is beyond its equilibrium point, so will want to accelerate back towards E
    • draw an acceleration arrow to show this initial acceleration
    • the initial acceleration is not zero (but the initial speed is, as it's released from rest)

• The two equations to find the initial acceleration are:
  • from Newton's 2nd Law upwards
    • here, the order matters (resolve upwards, as it's moving in that direction)
  • from Hooke's Law
• After that initial release, the particle oscillates about the equilibrium position, E (not about its natural length)
  • the maximum speed is when it passes through E
    • at this point, it's acceleration is zero
  • Springs lead to full oscillations (assuming it doesn't hit the ceiling), but strings may become slack if the initial extension is very large
    
    • in particular, they become slack when the extension is zero (at its natural length)
    • after this point, the particle moves freely like a projectile under gravity
• The same theory can be applied to strings and springs on smooth or rough inclined planes