Oblique Collisions with a Surface (Edexcel A Level Further Maths: Further Mechanics 1)

Revision Note

Test Yourself

Author

Paul

Expertise

Maths

Oblique Collisions with a Surface

What are oblique collisions (with a surface)?

In a normal collision a particle collides with a surface at right angles
In an oblique collision the angle at which the particle collides with the surface is not 90°
In oblique collisions
- there are two dimensions of motion of the particle to consider
- the velocity of the particle will change and so its momentum will change
- this is caused by an impulse from the surface to the particle
  - the impulse acts perpendicular to the surface

diagram demonstrating difference between a normal collision and oblique collision

What modelling assumptions are used for oblique collisions?

Problems are usually presented with a diagram in plan view (i.e. from above)
Modelling assumptions
- the surface the particle is moving across ('the floor') is horizontal
- the surface the particle will collide with ('the wall') is flat and fixed
- the 'floor' and 'wall' are smooth (no friction)
- particles are usually smooth spheres
  - this is so that the impact of the collision can be considered as occurring at a single point in space

What equations are needed to solve oblique collision problems?

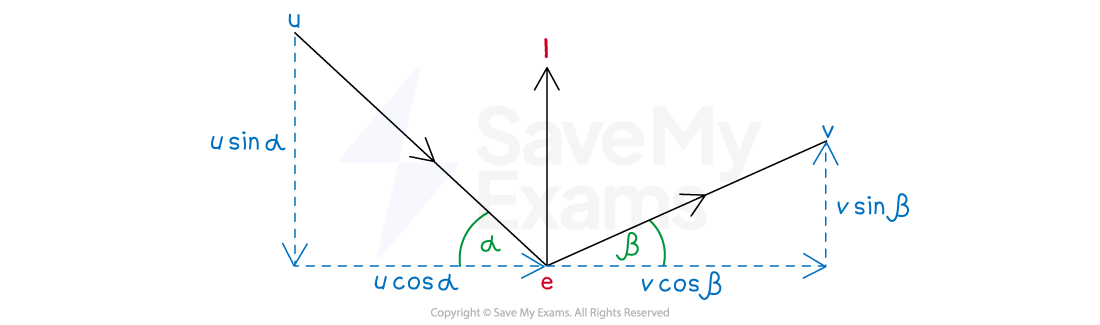
diagram of oblique collision with angles and velocity components labelled

In the diagram
- $u$ m s^-1 is the velocity before impact, $v$ m s^-1is the velocity after impact
- $α$ ° is the angle of approach, $β$ ° is the angle of rebound
- $I$ N is the impulse (which always acts perpendicular to the surface)
- $e$ is the coefficient of restitution (between the particle and the surface)
The component of velocity parallel to the surface remains unchanged
- - $v \cos β = u \cos α$
The component of velocity perpendicular to the surface can be found by applying Newton's Law of Restitution
- $\begin{array}{rcl} e & = & \frac{v \sin β}{u \sin α} \end{array}$
- Rearranging
  - $\begin{array}{rcl} v \sin β & = & e u \sin α \end{array}$
Dividing the above two equations eliminates $u$ and $v$
- $\tan β = e \tan α$
- Since $0 \leq e \leq 1$ it follows that $\tan β \leq \tan α$ and so $β \leq α$
  (i.e. angle of rebound is less than or equal to the angle of approach)

How do I solve oblique collision problems?

STEP 1
Draw a diagram (or add to a given one) showing important information in the question such as velocity/speed of approach/rebound, angle of approach/rebound, impulse
STEP 2
Write an equation for the motion parallel to the surface using $v \cos β = u \cos α$
Write an equation for the motion perpendicular to the surface using $v \sin β = e u \sin α$
STEP 3
Using "square and add" and/or "division" to eliminate unwanted quantities
( $v \tan β = e u \tan α$ can be used directly)
STEP 4
Answer the question by solving the relevant equation(s) for the required quantity

Exam Tip

Problems will often refer to the speed (rather than velocity) of the particle before and/or after the collision
- This can be confusing but speed is the magnitude of velocity and so has components parallel and perpendicular to the surface
Do not assume all surfaces ('walls') are orientated in a 'nice' direction
- e.g. parallel to the x- or y-axes in an xy plane, or parallel to the i or j vectors in a vector problem
- In questions given in vector form the direction of the impulse is often needed before the orientation of the surface can be deduced
- impulse is perpendicular to the surface
- draw, and if necessary, redraw, a diagram to help visualise the problem

Worked example

A smooth sphere is rolling across a smooth horizontal floor with speed 18 m s^-1 when it collides with a smooth, fixed vertical wall. The angle of the collision with the wall is 52° and the coefficient of restitution between the floor and the wall is 0.45.

Trajectory of a particle colliding with a wall at 52 degrees and rebounding

Find, the speed of the sphere immediately after the collision.

worked solution to an oblique collision with a surface

Using Scalar Product with Collisions

The scalar product

The scalar product is defined as $a \cdot b = a b \cos θ$ where $θ$ is the angle between the vectors $a$ and $b$ , and $a$ and $b$ are the magnitudes of those vectors respectively.

diagram showing oblique collision with wall direction and perpendicular (impulse) direction labelled

In the diagram above

$P$ is a vector that is perpendicular to the surface and so is in the direction of the impulse
$P$ could, but isn't necessarily, equal to the impulse $I$
$W$ is a vector that is parallel to (in the direction of) the surface

Applying the scalar product perpendicular to the surface

Consider $u \cdot P$
- $u \cdot P = u P \cos (90 + α)$
- Since $\cos (90 + α) = - \sin α$ this leads to the result
  $u \cdot P = - u P \sin α$
Similarly, for $v . P$
- $v \cdot P = v P \cos (90 - β)$
- Since $\cos (90 - β) = \sin β$ this leads to the result
  $v \cdot P = v P \sin β$
Combining these two results with $v \sin β = e u \sin α$ gives
- $\frac{v \cdot P}{P} = - e \frac{u \cdot P}{P}$
- So, $v \cdot P = - e u \cdot P$
- As the impulse ( $I$ ) is always perpendicular to the surface, if the direction of the surface ( $W$ ) is known then the direction of the impulse ( $P$ ) can be written down, and vice versa

Applying the scalar product parallel to the surface

Now consider $u \cdot W$
- $u \cdot W = u W \cos α$
Similarly, for $v \cdot W$
- $v \cdot W = v W \cos β$
Combining these two results with $v \cos β = u \cos α$ gives
- $\frac{v \cdot W}{W} = \frac{u \cdot W}{W}$
- So, $v \cdot W = u \cdot W$

How do I use the scalar product to solve oblique collision problems?

The scalar product approach should be used when questions give velocities/impulse/etc in vector form
- If magnitude (speed) and angles are given, using the techniques in the revision notes above are usually easier to apply
Using the scalar product is particularly suited to problems where the surface is not simply parallel to $i$ or $j$
Ensure you are familiar with the two formulae
$v \cdot P = - e u \cdot P$ and
$v \cdot W = u \cdot W$
For problems where the direction of the surface is not parallel to $i$ or $j$ use the fact that the direction of the impulse ( $P$ ) and the direction of the fixed surface ( $W$ ) are perpendicular
- So if $P = x i + y j$ then $W = y i - x j$ (and vice versa)
- To find an unknown $P$ or $W$ , use both dot product equations to set up simultaneous equations in $x$ and $y$
In some problems it may be necessary to use the impulse-momentum principle to find the impulse, $I$
(and so its direction $P$ )
$I = m (v - u)$
STEP 1
Draw a diagram, or add to a given one
Consider whether the direction of the fixed surface ( $W$ ) and/or the direction of the impulse ( $P$ ) are known
One can be determined from the other
Depending on the information given, $I = m (v - u)$ may be needed to find the direction of the impulse ( $P$ )
STEP 2
Determine which information is given and required, and use this to select one or both of the scalar product equations
STEP 3
Use the scalar product to set up equation(s) in the unknown(s) required
STEP 4
Solve the equations and hence solve the problem

Exam Tip

The use of scalar product may seem very complicated at first, especially with the notation used
- It is worth spending some time learning and becoming familiar with these formulae though as they can greatly reduce the amount of work required to gain lots of marks!

Worked example

A small smooth sphere is moving with velocity $(- 4 i + 4 j) m s^{- 1}$ across a smooth horizontal plane. It collides with a smooth fixed, vertical plane that lies in the direction $(2 i + 3 j)$ . The coefficient of restitution between the sphere and the vertical plane is 0.1.

Find the velocity of the sphere immediately after it collides with the vertical plane.

worked solution to oblique collisions problem using scalar product

Successive Collisions in 2D

How do I solve problems involving successive collisions in 2D?

diagram showing successive oblique collisions with angled surfaces

Successive collisions are where a particle collides with one fixed surface, then another
The modelling assumption that the particle, the plane it is travelling in, and the fixed surface(s) it collides with are all smooth mean that the velocity/speed of rebound from the first collision will be the velocity/speed of the approach in the second collision
The two fixed surfaces the particle collides with may, or may not, be perpendicular to each other
- the cushions on a snooker table are perpendicular
The coefficients of restitution between the particle and each of the fixed surfaces may or may not be equal
- read the information given in the question carefully
Separate the collisions into two single collision problems
- Draw and label a diagram for each collision
Use the scalar product approach where possible
- This is often easiest when velocities, etc have been given as vectors

Worked example

Two fixed, smooth vertical walls meet at an angle of 100° on a smooth horizontal surface. A smooth sphere is moving across the surface with speed 4 m s-¹ at an angle of 35° to the first wall and towards the intersection of the two walls. The coefficient of restitution between the sphere and the first wall is 0.4; for the second wall it is 0.8.

worked example question image of an object colliding with multiple surfaces at angles