Tension, Normal Force, Upthrust & Friction
- Tension:
The force experienced by a cable, rope, or string when pulled, hung, rotated or supported
- This is normally labelled as T on free body diagrams

Tension always acts away from the mass
- Normal Contact Force:
The force arising when an object rests against another object acting at a 90° angle to the plane of contact
- It is sometimes also referred to as the reaction force
- This is normally labelled as N or R on free body diagrams
- This force arises from Newton's Third Law
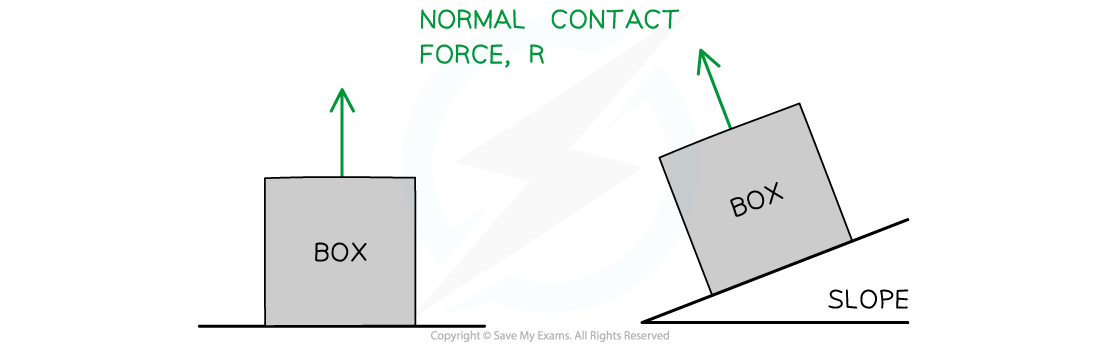
Normal contact force always acts perpendicular to the surface
- Upthrust:
The upward buoyancy force acting on an object when it is in a fluid
- Upthrust can occur in liquids and gases

Upthrust always acts upwards
- Friction:
The force that arises when two surfaces are in contact with each other
- Friction always opposes the motion
- This is normally labelled as F or Fr on free body diagrams

Friction always acts at the point where the objects are in contact, and in the opposite direction to the direction of motion





