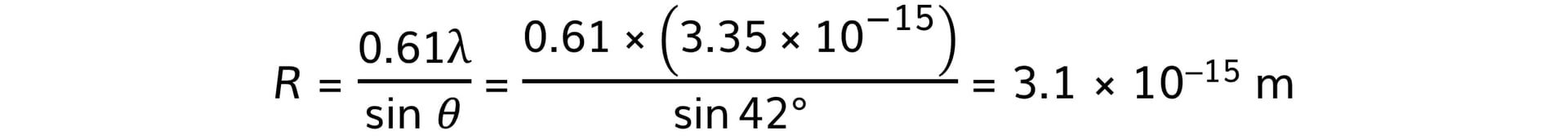8.3.4 Nuclear Radius

Closest Approach Method

• In the Rutherford scattering experiment, alpha particles are fired at a thin gold foil
• Some of the alpha particles are found to come straight back from the gold foil
• This indicates that there is electrostatic repulsion between the alpha particles and the gold nucleus

• At the point of closest approach, r, the repulsive force reduces the speed of the alpha particles to zero momentarily
• At this point, the initial kinetic energy of an alpha particle, E_k, is equal to electric potential energy, E_p
• The radius of the closest approach can be found be equating the initial kinetic energy to the electric potential energy

• Equating the two equations gives:

Pros & Cons of Closest Approach Method

Advantages

• Alpha scattering gives a good estimate of the upper limit for a nuclear radius
• The mathematics behind this approach are very simple
• The alpha particles are scattered only by the protons and not all the nucleons that make up the nucleus

Disadvantages

• This method does not give an accurate value for nuclear radius as it will always be an overestimate
  • This is because it measures the nearest distance the alpha particle can get to the gold nucleus, not the radius of it

• Alpha particles are hadrons, therefore, when they get close to the nucleus they are affected by the strong nuclear force and the mathematics do not account for this
• The gold nucleus will recoil as the alpha particle approaches
• Alpha particles have a finite size whereas electrons can be treated as a point mass
• It is difficult to obtain alpha particles which rebound at exactly 180°
  • In order to do this, a small collision region is required

• The alpha particles in the beam must all have the exact same initial kinetic energy
• The sample must be extremely thin to prevent multiple scattering

Electron Diffraction Method

• Electrons accelerated to close to the speed of light have wave-like properties such as the ability to diffract and have a de Broglie wavelength equal to:

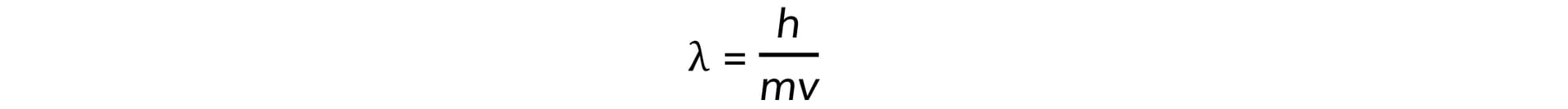
• Where:
  • h = Planck's constant
  • m = mass of an electron (kg)
  • v = speed of the electrons (m s⁻¹)

• The diffraction pattern forms a central bright spot with dimmer concentric circles around it
• From this pattern, a graph of intensity against diffraction angle can be used to find the diffraction angle of the first minimum
• Using this, the size of the atomic nucleus, R, can be determined from:

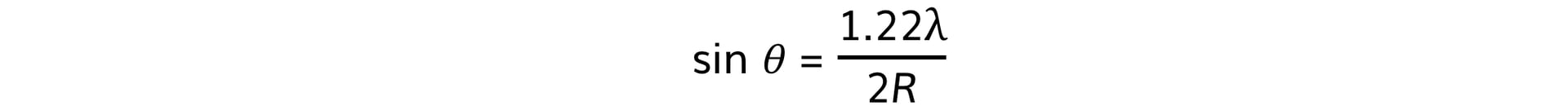
• Where:
  • θ = angle of the first minimum (degrees)
  • λ = de Broglie wavelength (m)
  • R = radius of the nucleus (m)

Pros & Cons of Electron Diffraction Method

Advantages

• Electron diffraction is much more accurate than the closest approach method
• This method gives a direct measurement of the radius of a nucleus
• Electrons are leptons; therefore, they will not interact with nucleons in the nucleus through the strong nuclear force as an alpha particle would

Disadvantages

• Electrons must be accelerated to very high speeds to minimise the de Broglie wavelength and increase resolution
  • This is because significant diffraction takes place when the electron wavelength is similar in size to the nuclear diameter

• Electrons can be scattered by both protons and neutrons
  • If there is an excessive amount of scattering, then the first minimum of the electron diffraction can be difficult to determine

• The graph of intensity against angle obtained through electron diffraction is as follows:

Step 1: Identify the first minimum from the graph

• Angle of first minimum, θ = 42°

Step 2: Write out the equation relating the angle, wavelength, and nuclear radiusStep 3: Calculate the nuclear radius, R