The network shown below displays the distance, in metres, of the cables in a network between different connection points A, B, C, D, E and F.
Each length of cable must be inspected.
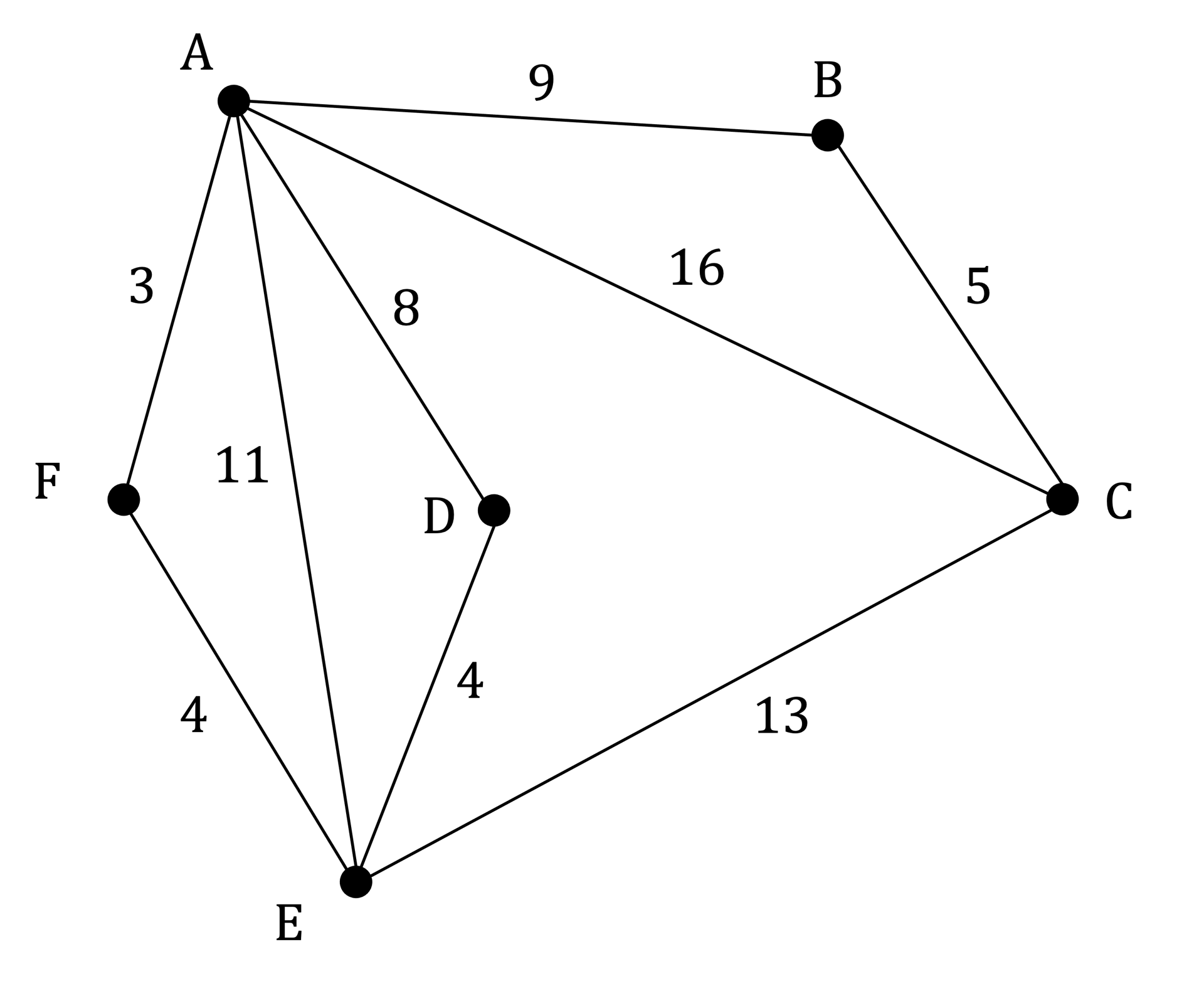
a)
Find the shortest route that starts and finishes at connection point E.
- STEP 1
Inspect the order of the nodes
A: 5 (odd)
B: 2 (even)
C: 3 (odd)
D: 2 (even)
E: 4 (even)
F: 2 (even)
- STEP 2
There is exactly one pair of odd vertices, A and C
The shortest route between A and C is ABC so the edges AB and BC need repeating
An Eulerian circuit, starting and ending at connection point E, is now possible
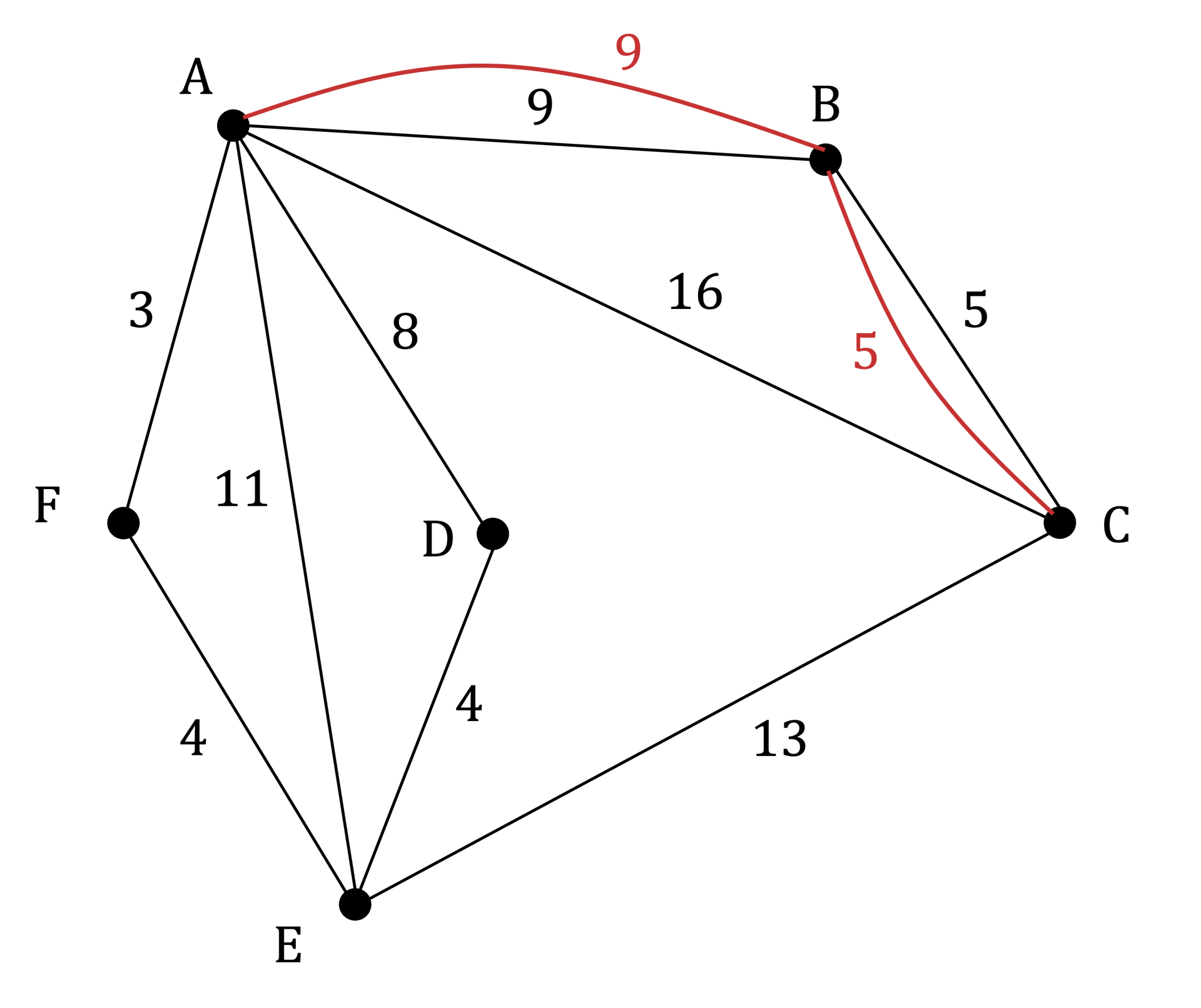
- STEP 3
Find an Eulerian circuit, starting and ending at connection point E
Shortest route: EFAEDABACBCE
b)
State the total length of the shortest route.
Add together the lengths of the edges in the original graph
3 + 4 + 4 + 5 + 8 + 9 + 11 + 13 + 16 = 73
Add the result to the lengths of the repeated edges
73 + 5 + 9 = 87
Shortest route = 87 km



