Collisions & Explosions
- In both collisions and explosions, momentum is always conserved
- However, kinetic energy might not always be
- A collision (or explosion) is either:
- Elastic – if the kinetic energy is conserved
- Inelastic – if the kinetic energy is not conserved
- Collisions are when objects strike against each other
- Elastic collisions are commonly those where objects colliding do not stick together and then move in opposite directions
- Inelastic collisions are commonly those where objects collide and stick together after the collision
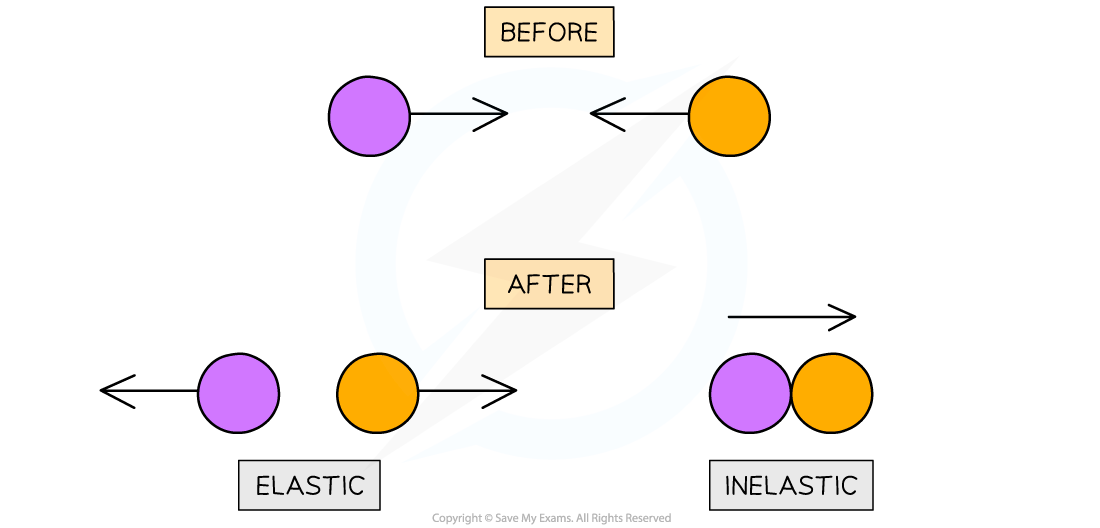
Elastic collisions are where two objects move in opposite directions. Inelastic collisions are where two objects stick together
- An explosion is commonly to do with recoil
- For example, a gun recoiling after shooting a bullet or an unstable nucleus emitting an alpha particle and a daughter nucleus
- To find out whether a collision is elastic or inelastic, compare the kinetic energy before and after the collision
- The equation for kinetic energy is:

Worked example
Two similar spheres, each of mass m and velocity v are travelling towards each other. The spheres have a head-on elastic collision.What is the total kinetic energy after the impact?

Worked example
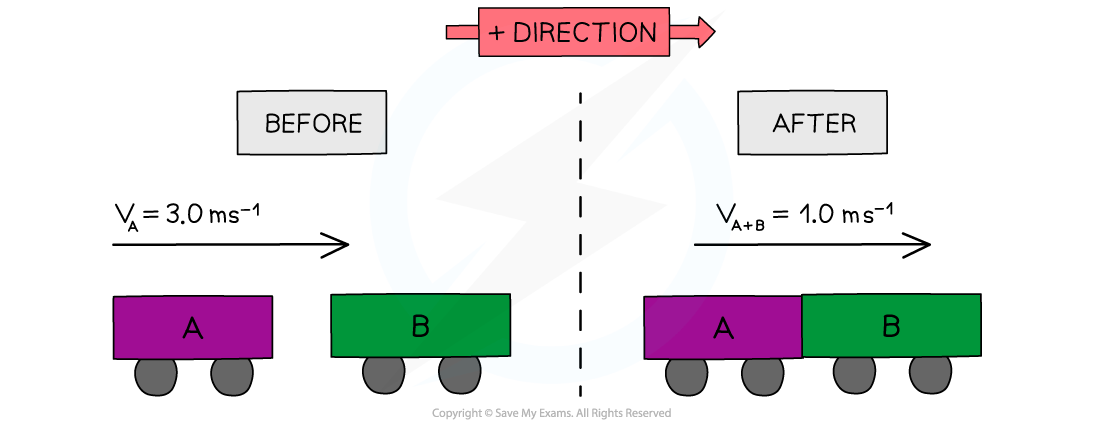
Trolley A of mass 0.80 kg collides head-on with stationary trolley B at speed 3.0 m s–1. Trolley B has twice the mass of trolley A.The trolleys stick together and travel at a velocity of 1.0 m s–1.Determine whether this is an elastic or inelastic collision.

Exam Tip
If an object is stationary or at rest, its velocity equals 0, therefore, the momentum and kinetic energy are also equal to 0When a collision occurs in which two objects are stuck together, treat the final object as a single object with a mass equal to the sum of the two individual objectsDespite velocity being a vector, kinetic energy is a scalar quantity and therefore will never include a minus sign - this is because in the kinetic energy formula, mass is scalar and the v2 will always give a positive value whether its a negative or positive velocity




