Applying Newton’s Laws of Motion
- Newton's laws of motion are strong tools to understand the motion of objects with forces acting upon them
- Below are two worked examples demonstrating different situations involving the application of Newton's laws
Worked example
Two blocks of mass 1 kg and 4 kg respectively are attached by a tight massless rope between them. The 1 kg block sits on the left and the 4 kg block sits on the right. The 1 kg mass has a 100 Newton force applied to it pulling it to the left. What is the acceleration of both blocks and the tension in the rope as they move across a frictionless surface?
A The acceleration is 15 m s–2 to the left and the tension is 20 N
B The acceleration is 20 m s–2 to the left and the tension is 40 N
C The acceleration is 15 m s–2 to the left and the tension is 60 N
D The acceleration is 20 m s–2 to the left and the tension is 80 N
Step 1: Consider the whole of the system
- Together the 1 kg and 4 kg blocks are both being pulled along by the 100 N force (since the rope is tight)
- This is a frictionless flat surface, therefore the only forces in the system are the pulling force and the tension force(s) in the rope
- Therefore the acceleration can be found using Newton's second law

Step 2: Find the acceleration
-
- Using Newton's second law:
F = m × a
-
- Rearrange for a
a = F ÷ m
a = 100 ÷ 5 = 20 m s–2 to the left
Step 3: Examine the 4 kg mass only
-
- Since the system is moving with an acceleration of 20 m s–2 to the left, the force on only the 4 kg mass can be found
F = m × a
F = 4 × 20 = 80 N to the left
-
- The only force acting on the 4 kg mass is the rope and therefore tension force
- This means there is 20 N pulling force on the 1 kg block only
Step 4: State your answer
-
- Since acceleration, a = 20 m s–2 to the left and the tension force = 80 N to the left
- Therefore, the answer is option D
Worked example
A stationary object is subject to a 300 N force towards the left and at 55 degrees leftwards with respect to the vertical and a 450 N force to the right and 35° downwards with respect to the horizontal.Calculate what is the magnitude and direction of the third force that would make this object remain stationary (to the nearest N).
Step 1: Recall Newton's first law
- Newton's First Law states:
A body will remain at rest or move with constant velocity unless acted on by a resultant force
- Therefore, for this object to remain stationary, the resultant force must have a magnitude of 0 Newtons
Step 2: Resolve the 300 N force into its horizontal and vertical components
-
- The horizontal component can be resolved from:
sin(55°) × 300 = 246 N
-
- This is directed to the left
-
- The vertical component can be resolved from:
cos(55°) × 300 = 172 N
-
- This is in an upwards direction

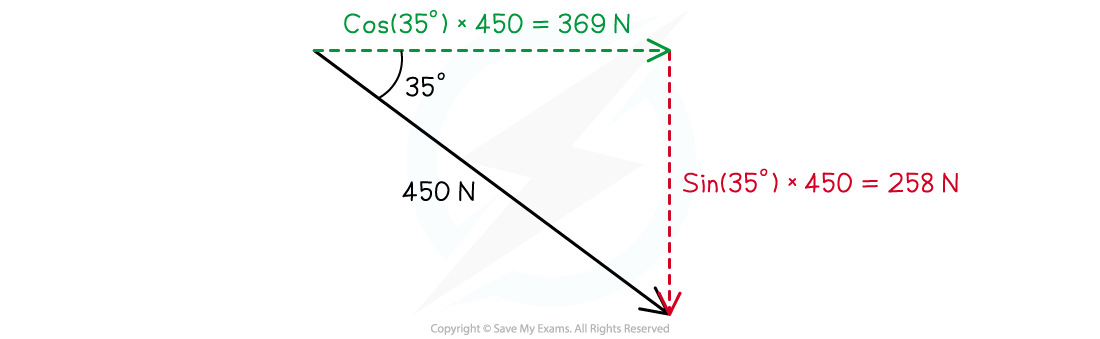
Step 3: Resolve the 450 N force into its horizontal and vertical components
- The horizontal component can be resolved from:
cos(35°) × 450 = 369 N
- This is directed to the right
- The vertical component can be resolved from:
sin(35°) × 450 = 258 N
- This is in a downwards direction
Step 4: Combine the horizontal components
- The two forces provide 369 N to the right and 246 N to the left
- Therefore, since these are opposing directions:
369 – 246 = 123 N to the right
Step 5: Combine the vertical components
- The two forces provide 258 N downwards and 172 N upwards
- Therefore, since these are opposing directions:
258 – 172 = 86 N downwards
Step 6: Make a right angle triangle using these two force vectors
-
- There should be a longer size 123 N magnitude vector arrow to the right and then a 86 N magnitude vector arrow downwards
- These can be connected from start to finish by a third vector which is the hypotenuse of this right-angled triangle

Step 7: Use the two vectors magnitudes to find the angle from the horizon
-
- Since the vectors are to the right and downwards in this right-angle triangle, neither is the hypotenuse
- Therefore the angle from the horizontal downwards can be found by using tan:
tan(θ°) = Opp. ÷ Adj. = 86 ÷ 123
θ° = tan–1(86 ÷ 123) = tan–1(0.699)
θ° ≈ 35°
Step 8: Use Pythagoras theorem or trigonometry to find the magnitude of the resultant force acting on the object
-
- Method 1: Using Pythagoras theorem
- c2 = b2 + a2 where b and a are the vector magnitudes for the horizontal and vertical components found so far and c is the hypotenuse magnitude
- Method 1: Using Pythagoras theorem
c2 = 862 + 1232 = 7396 + 15129 = 22525
c = √22 525 ≈ 150 N
-
- Method 2: Using trigonometry
- Using the horizontal component and the angle found in step 7, cos can be used
- Method 2: Using trigonometry
cos(35°) = Adj. ÷ Hyp. = 123 ÷ Hyp.
-
-
- Therefore:
-
123 ÷ cos(35°) = Hyp. ≈ 150 N
Step 9: State the final answer
-
- The third force which would cause this object to remain stationary is equal and opposite to the resultant force acting on the object
- Therefore the force required is 150 N left and 35° upwards from the horizontal
Exam Tip
You are expected to know Newton's three laws of motion from memory and how they apply to physical situations. So be sure to practice and use them without having to review them before carrying out a problem.

