Newton-Raphson Method (Edexcel International A Level Further Maths)

Newton-Raphson Method

How do I apply the Newton-Raphson method?

• The Newton-Raphson method is a process for finding roots of equations

  • Equations must be rearranged into the form

• If is a root of the equation , then you need to choose , the initial (first) approximation

  • This is usual given in the question (and is a value near to the root)

• You can then find successive approximations , , , ... using the Newton-Raphson formula:

  • 

  • This is an iterative formula

  • is the derivative of

    • Work this out beforehand

• Increasing the number of approximations improves the accuracy

  • The Newton-Raphson method usually converges quickly to the root compared to other methods

How do I apply the Newton-Raphson method on my calculator?

• If your calculator has a recursion function

  • Input the formula, start value and number of steps

  • The output is a table showing all the approximations

• Alternatively:

  • Type in the value of and press =

    • This stores it in the "Ans" (answer) button

  • Type into your calculator and press =

    • This finds

  • Without pressing any other button, press = again

    • This finds

  • Repeatedly pressing = gives further approximations

    • The more you press it, the closer to the root it becomes

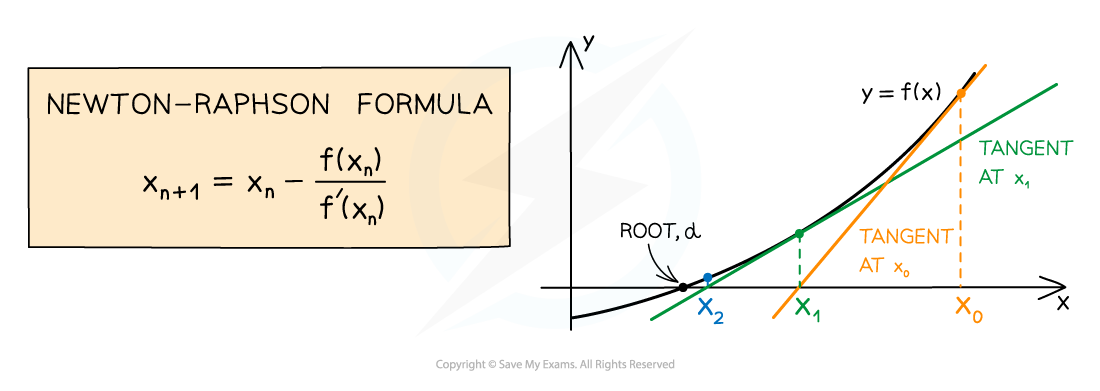
How does the Newton-Raphson method work geometrically?

• The method works by drawing a tangent to the curve at

  • then finding where the tangent cuts the x-axis

  • This x-intercept is the new approximation,

• This process is then repeated

  • Draw the tangent to at

  • Find its x-intercept and call it

• The approximations get closer and closer to the root

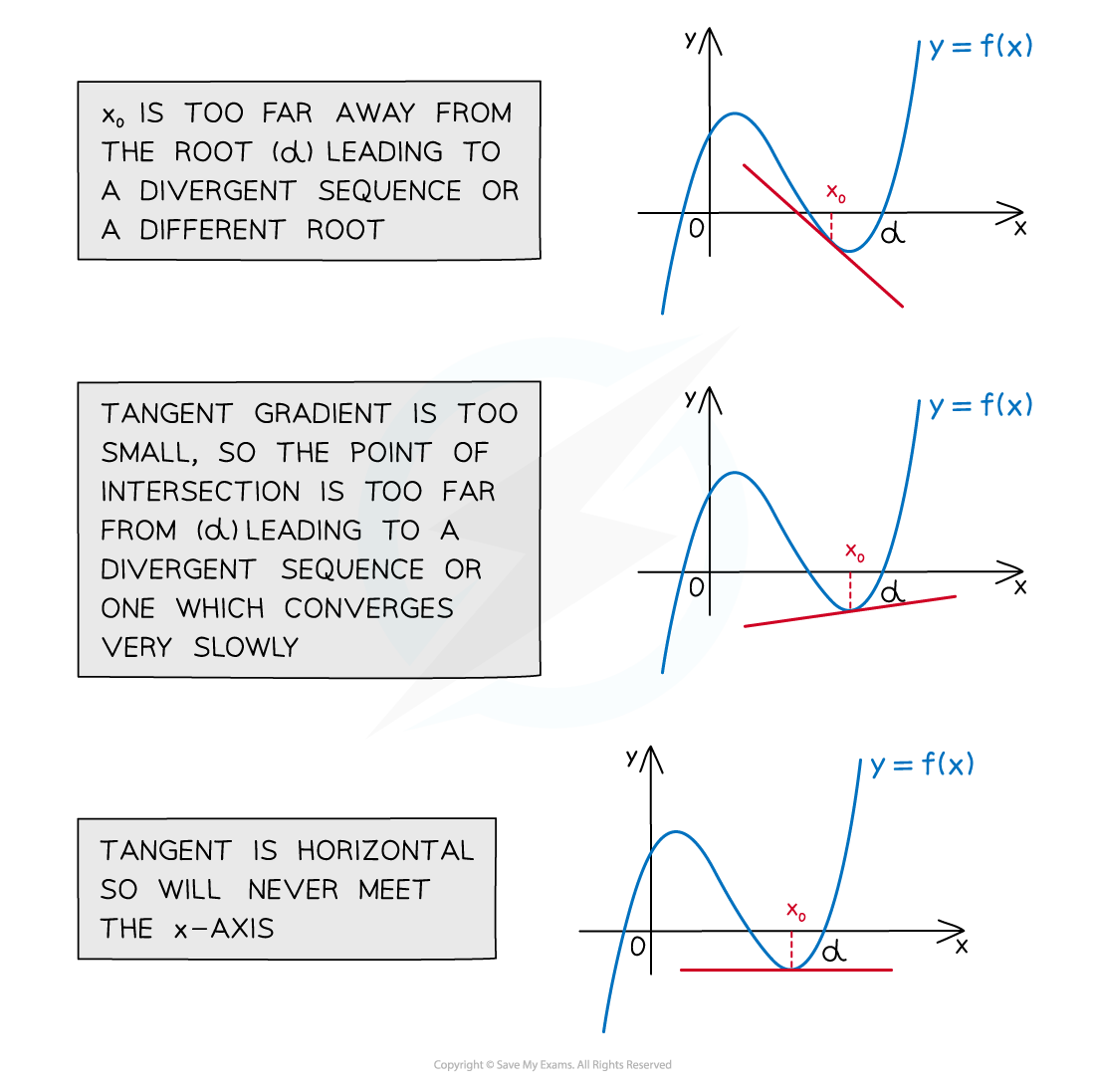
How do I know if the Newton-Raphson method will fail?

• The Newton-Raphson method fails if the initial value, , satisfies

  • Algebraically, this is because the formula cannot divide by zero

  • Geometrically, this is because is at a stationary point on the curve

    • A tangent drawn at a stationary point is horizontal

    • This will never intersect the x-axis

• The Newton-Raphson method also fails if the sequence , , , ... diverges

  • This can happen if is chosen:

    • too far away from the root

    • or at a point where the gradient is very small

• The Newton-Raphson method is sometimes avoided when is too tricky to differentiate