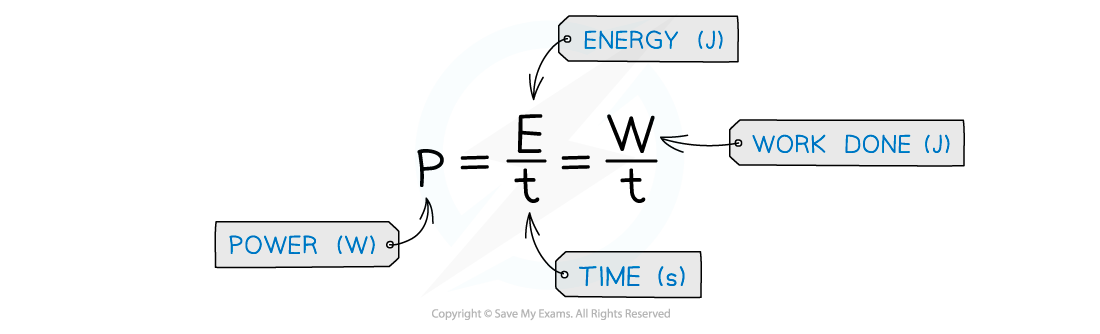
Power
- The power of a machine is the rate at which it transfers energy
- Since work done is equal to the energy transferred, power can also be defined as the rate of doing work or the work done per unit time
- The SI unit for power is the Watt (W)
- Power is also used in electricity, with labels on lightbulbs which indicate their power, such as 60 W or 100 W
- These indicate the amount of energy transferred by an electrical current rather than by a force doing work
The Watt
- The Watt, W, is commonly used as the unit power (and radiant flux)
- It is defined as 1 W = 1 J s-1
- The SI unit for energy is kg m2 s–3
- One watt is defined as:
A transfer of energy of 1 J in 1 s
Worked example
A car engine exerts the following force for 1.0 km in 200 s. What is the average power developed by the engine?
What is the average power developed by the engine?

Exam Tip
Think of power as “energy per second”. Thinking of it this way will help you to remember the relationship between power and energy: “Watt is the unit of power?”


 The lorry has a mass of 3500 kg and is travelling at a constant speed of 9.4 m s-1. The force due to air resistance is negligible.Calculate the useful power from the engine to move the lorry up the road.
The lorry has a mass of 3500 kg and is travelling at a constant speed of 9.4 m s-1. The force due to air resistance is negligible.Calculate the useful power from the engine to move the lorry up the road.

