Newton's Second Law
- Newton's Second Law states:
The resultant force is equal to the rate of change in momentum. The change in momentum is in the same direction as the resultant force
- This can also be written as:
- This relationship means that objects will accelerate if there is a resultant force acting upon them
- This is derived from the definition of momentum as follows:

- An unbalanced force on a body means it experiences a resultant force
- If the resultant force is along the direction of motion, it will speed up (accelerate) or slow down (decelerate) the body
- If the resultant force is at an angle, it will change the direction of the body
Worked example
A girl is riding her skateboard down the road and increases her speed from 1 m s–1 to 4 m s–1 in 2.5 s.If the force driving her forward is 72 N, calculate the combined mass of the girl and the skateboard.

Resultant Force
- Since force is a vector, every force on a body has a magnitude and direction
- The resultant force is, therefore, the vector sum of all the forces acting on the body
- The direction is given by either the positive or negative direction as shown in the examples below

Resultant forces on a body can be positive or negative depending on their direction
- The resultant force could also be at an angle, in which case, the magnitude and direction of the resultant force can be determined using either:
- Calculation (usually simple geometry, such as Pythagoras Theorem or the sine and cosine rules)
- Scale drawing
Acceleration
- Since acceleration is a vector, it can be either positive or negative depending on the direction of the resultant force
- If the resultant force is in the same direction as the motion of an object, the acceleration is positive
- If the resultant force is in the opposite direction to the motion of an object, the acceleration is negative
- An object may continue in the same direction however with a resultant force in the opposite direction to its motion, it will slow down and eventually come to a stop
- If drag forces are ignored, or severely reduced, the acceleration is independent of the mass of an object
- This has been shown in experiments by astronauts who have dropped a feather and a hammer on the Moon from the same height
- Both the hammer and feather drop to the Moon's surface at the same time
Worked example
Three forces, 4 N, 8 N, and 24 N act on an object with a mass of 5 kg. Which acceleration is not possible with any combination of these three forces?
A. 1 m s–2
B. 4 m s–2
C. 7 m s–2
D. 10 m s–2
Step 1: List the values given
-
- Three possible forces at any angle of choice: 4 N, 8 N, and 24 N
- Mass of object = 5 kg
Step 2: Consider the relevant equation
-
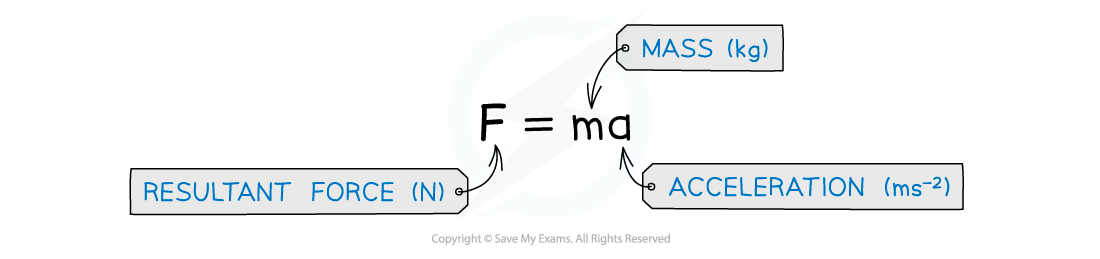
- Newton's second law:
F = m × a
Step 3: Rearrange to make acceleration the focus
a = F ÷ m
Step 4: Investigate the minimum possible acceleration
-
- It is best to consider the edges of this problem before dealing with more difficult combinations that is why it is prudent to check the minimum and maximum acceleration
- The minimum would occur when the forces were acting against each other
- The minimum possible would be when only the 4 N force was acting on the body
- Now check the acceleration:
4 N ÷ 5 kg = 0.8 m s–2
Step 5: Investigate the maximum possible acceleration
-
- The maximum would occur when all three forces are acting in the same direction
- Therefore adding to:
4 + 8 + 24 = 36 N
-
- Now check the acceleration:
36 N ÷ 5 kg = 7.2 m s–2
Step 6: Consider this range and the options
-
- Since option D is higher than 7.2 m s–2; it is not possible that these three forces can produce 10 m s–2 acceleration for this mass
- Option D is the correct answer
Worked example
A rocket produces an upward thrust of 15 MN and has a weight of 8 MN.
A. When in flight, the force due to air resistance is 500 kN.
Determine what is the resultant force on the rocket.
B. The mass of the rocket is 0.8 × 105 kg.
Calculate the magnitude and direction of the acceleration of the rocket.


Exam Tip
The direction you consider positive is your choice, as long as the signs of the numbers (positive or negative) are consistent throughout the question.It is a general rule to consider the direction the object is initially travelling in as positive. Therefore all vectors in the direction of motion will be positive and opposing vectors, such as drag forces, will be negative.