Origin of the Forces Between Current-Carrying Conductors
- A current carrying conductor, such as a wire, produces a magnetic field around it
- The direction of the field depends on the direction of the current through the wire
- This is determined by the right hand thumb rule
- Parallel current-carrying conductors will therefore either attract or repel each other
- If the currents are in the same direction in both conductors, the magnetic field lines between the conductors cancel out – the conductors will attract each other
- If the currents are in the opposite direction in both conductors, the magnetic field lines between the conductors push each other apart – the conductors will repel each other

Both wires will attract if their currents are in the same direction and repel if in opposite directions
- When the conductors attract, the direction of the magnetic forces will be towards each other
- When the conductors repel, the direction of the magnetic forces will be away from each other
- The magnitude of each force depend on the amount of current and length of the wire
Worked example
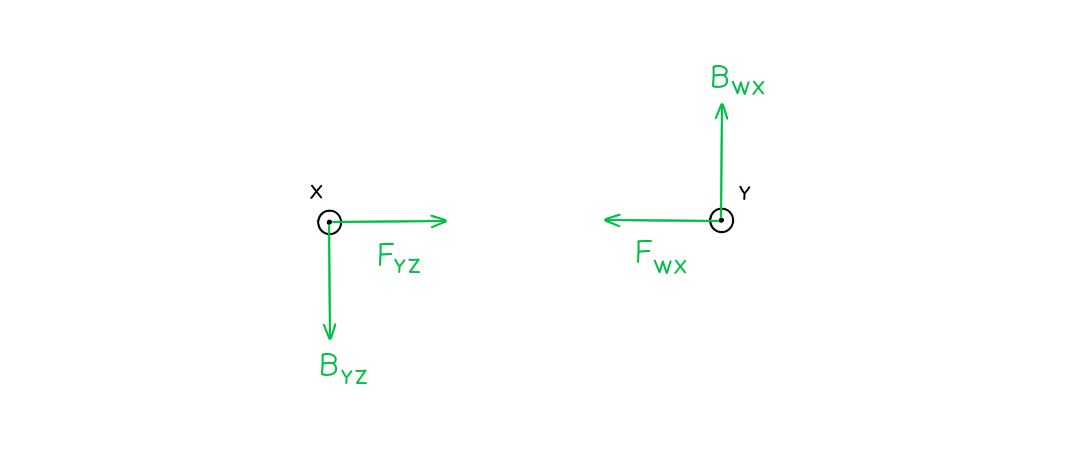
Two long, straight, current-carrying conductors, WX and YZ, are held at a close distance, as shown in diagram 1. The conductors each carry the same magnitude current in the same direction. A plan view from above the conductors is shown in diagram 2.
The conductors each carry the same magnitude current in the same direction. A plan view from above the conductors is shown in diagram 2. On diagram 2, draw arrows, one in each case, to show the direction of:
On diagram 2, draw arrows, one in each case, to show the direction of:
- The magnetic field at X due to the current in wire YZ (label this arrow BYZ)
- The force at X as a result of the magnetic field due to the current in the wire YZ (label this arrow FYZ)
- The magnetic field at Y due to the current in wire WX (label this arrow BWX)
- The force at Y as a result of the magnetic field due to the current in the wire WX (label this arrow FWX)
- Newton’s Third Law states:
- When two bodies interact, the force on one body is equal but opposite in direction to the force on the other body
- Therefore, the forces on the wires act in equal but opposite directions

