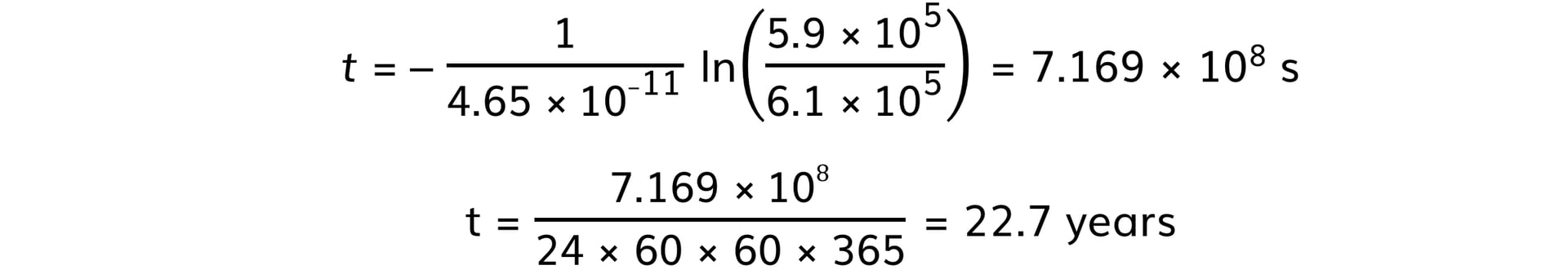8.2.2 Exponential Decay

• In radioactive decay, the number of undecayed nuclei falls very rapidly, without ever reaching zero
  • Such a model is known as exponential decay

• The graph of number of undecayed nuclei against time has a very distinctive shape:

Radioactive decay follows an exponential pattern. The graph shows three different isotopes each with a different rate of decay

• The key features of this graph are:
  • The steeper the slope, the larger the decay constant λ (and vice versa)
  • The decay curves always start on the y-axis at the initial number of undecayed nuclei (N₀)

Equations for Radioactive Decay

• The number of undecayed nuclei N can be represented in exponential form by the equation:

N = N₀ e^–λt

• Where:
  • N₀ = the initial number of undecayed nuclei (when t = 0)
  • N = number of undecayed nuclei at a certain time t
  • λ = decay constant (s^-1)
  • t = time interval (s)

• The number of nuclei can be substituted for other quantities.
• For example, the activity A is directly proportional to N, so it can also be represented in exponential form by the equation:

A = A₀ e^–λt

• Where:
  • A = activity at a certain time t (Bq)
  • A₀ = initial activity (Bq)

• The received count rate C is related to the activity of the sample, hence it can also be represented in exponential form by the equation:

C = C₀ e^–λt

• Where:
  • C = count rate at a certain time t (counts per minute or cpm)
  • C₀ = initial count rate (counts per minute or cpm)

The exponential function e

• The symbol e represents the exponential constant
  • It is approximately equal to e = 2.718

• On a calculator it is shown by the button e^x
• The inverse function of e^x is ln(y), known as the natural logarithmic function
  • This is because, if e^x = y, then x = ln(y)

Step 1: Write out the known quantities

• • Decay constant, λ = 0.025 year ^-1
  • Time interval, t = 5.0 years
  • Both quantities have the same unit, so there is no need for conversion

Step 2: Write the equation for activity in exponential form

A = A₀ e^–λt

Step 3: Rearrange the equation for the ratio between A and A₀

Step 4: Calculate the ratio A/A₀

Therefore, the activity of Strontium-90 decreases by a factor of 0.88, or 12%, after 5 years

Molar Mass

• The molar mass, or molecular mass, of a substance is the mass of a substance, in grams, in one mole
  • Its unit is g mol^-1

• The number of moles from this can be calculated using the equation:

Avogadro’s Constant

• Avogadro’s constant (N_A) is defined as:

The number of atoms in one mole of a substance; equal to 6.02 × 10²³ mol^-1

• For example, 1 mole of sodium (Na) contains 6.02 × 10²³ atoms of sodium
• The number of atoms, N, can be determined using the equation:

Part (a)

Step 1: Write down the known quantities

• • Mass = 5.1 μg = 5.1 × 10^-6 g
  • Molecular mass of americium = 241

Step 2: Write down the equation relating number of nuclei, mass and molecular mass

• • where N_A is the Avogadro constant

Step 3: Calculate the number of nuclei

Part (b)

Step 1: Write down the known quantities

• • Activity, A = 5.9 × 10⁵ Bq
  • Number of nuclei, N = 1.27 × 10¹⁶

Step 2: Write the equation for activity

Activity, A = λN

Step 3: Rearrange for decay constant λ and calculate the answer

Part (c)

Step 1: Write down the known quantities

• • Activity, A = 5.9 × 10⁵ Bq
  • Initial activity, A₀ = 6.1 × 10⁵ Bq
  • Decay constant, λ = 4.65 × 10^–11 s^–1

Step 2: Write the equation for activity in exponential form

A = A₀ e^–λt

Step 3: Rearrange for time t

Step 4: Calculate the age of the smoke detector and convert to years

• • Therefore, the smoke detector is 22.7 years old