Radians
- In circular motion, it is more convenient to measure angular displacement in units of radians rather than units of degrees
- The angular displacement (θ) of a body in circular motion is defined as:
The change in angle, in radians, of a body as it rotates around a circle
- The angular displacement is the ratio of:

- Note: both distances must be measured in the same units e.g. metres
- A radian (rad) is defined as:
The angle subtended at the centre of a circle by an arc equal in length to the radius of the circle
- Angular displacement can be calculated using the equation:


When the angle is equal to one radian, the length of the arc (Δs) is equal to the radius (r) of the circle
- Where:
- Δθ = angular displacement, or angle of rotation (radians)
- s = length of the arc, or the distance travelled around the circle (m)
- r = radius of the circle (m)
- Radians are commonly written in terms of π
- The angle in radians for a complete circle (360o) is equal to:
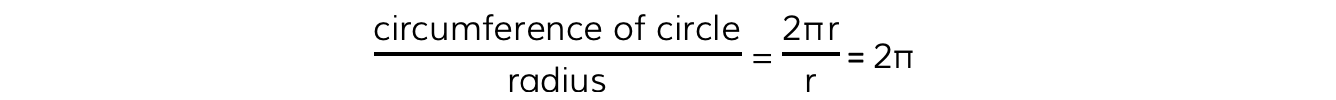
Radian Conversions
- If an angle of 360o = 2π radians, then 1 radian in degrees is equal to:

- Use the following equation to convert from degrees to radians:
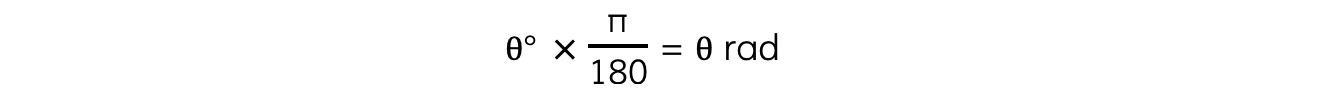
Table of common degrees to radians conversions
Worked example
Convert the following angular displacement into degrees:

Exam Tip
- You will notice your calculator has a degree (Deg) and radians (Rad) mode
- This is shown by the “D” or “R” highlighted at the top of the screen
- Remember to make sure it’s in the right mode when using trigonometric functions (sin, cos, tan) depending on whether the answer is required in degrees or radians
- It is extremely common for students to get the wrong answer (and lose marks) because their calculator is in the wrong mode - make sure this doesn’t happen to you!
- This mode only matters if you're using sine, cos or tan

