4.7.4 The t-test

Test Yourself

Two-Sample Tests

What is a t-test?

A t-test is used to compare the means of two normally distributed populations
In the exam the population variance will always be unknown

What assumptions are needed for the t-test?

The underlying distribution for each variable must be normal
In the exam you will need to assume the variance for the two groups are equal
- You will need to use the pooled two-sample t-test

What are the steps for a pooled two-sample t-test?

STEP 1: Write the hypotheses
- H₀: μ_x= μ_y
  - Where μ_xand μ_yare the population means
  - Make sure you make it clear which mean corresponds to each population
  - In words this means the two population means are equal
- H₁: μ_x< μ_y or H₁: μ_x> μ_yor H₁: μ_x≠ μ_y
  - The alternative hypothesis will depend on what is being tested (see sections for one-tailed and two-tailed tests)
STEP 2: Enter the data into your GDC
- Enter two lists of data – one for each sample
- Choose the pooled option
- Your GDC will then give you the p-value
STEP 3: Decide whether there is evidence to reject the null hypothesis
- Compare the p-value with the given significance level
  - If p-value < significance level then reject H₀
  - If p-value > significance level then accept H₀
STEP 4: Write your conclusion
- If you reject H₀
  - There is sufficient evidence to suggest that the population mean of X is bigger than/smaller than/different to the population mean of Y
  - This will depend on the alternative hypothesis
- If you accept H₀
  - There is insufficient evidence to suggest that the population mean of X is bigger than/small than/different to the population mean of Y
  - Therefore this suggests that the population means are equal

One-tailed Tests

How do I perform a one-tailed t-test?

A one-tailed test is used to test one of the two following cases:
- The population mean of X is bigger than the population mean of Y
  - The alternative hypothesis will be: H₁: μ_x> μ_y
  - Look out for words such as increase, bigger, higher, etc
- The population mean of X is smaller than the population mean of Y
  - The alternative hypothesis will be: H₁: μ_x< μ_y
  - Look out for words such as decrease, smaller, lower, etc
If you reject the null hypothesis then
- This suggests that the population mean of X is bigger than the population mean of Y
  - If the alternative hypothesis is H₁: μ_x> μ_y
- This suggests that the population mean of X is smaller than the population mean of Y
  - If the alternative hypothesis is H₁: μ_x< μ_y

Worked example

The times (in minutes) for children and adults to complete a puzzle are recorded below.

Children	3.1	2.7	3.5	3.1	2.9	3.2	3.0	2.9
Adults	3.1	3.6	3.5	3.6	2.9	3.6	3.4	3.6	3.7	3.0

The creator of the puzzle claims children are generally faster at solving the puzzle than adults. A t-test is to be performed at a 1% significance level.

Write down the null and alternative hypotheses.

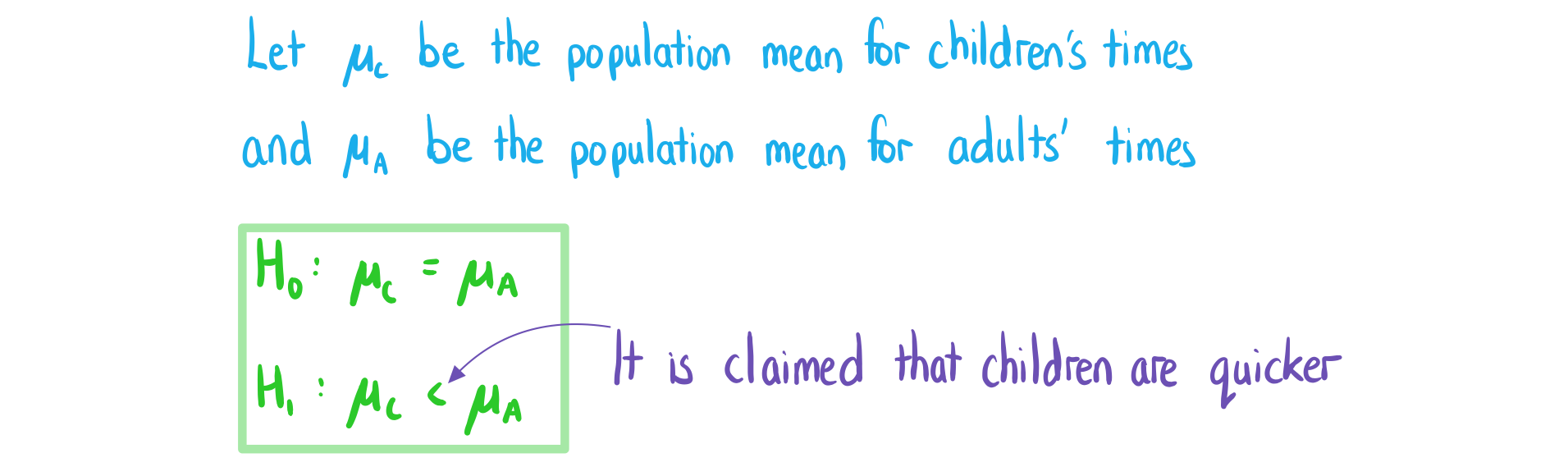
4-7-4-ib-ai-sl-t-test-one-tail-a-we-solution

Find the p-value for this test.

4-7-4-ib-ai-sl-t-test-one-tail-b-we-solution

State whether the creator’s claim is supported by the test. Give a reason for your answer.

4-7-4-ib-ai-sl-t-test-one-tail-c-we-solution

Two-tailed Tests

How do I perform a two-tailed t-test?

A two-tailed test is used to test the following case:
- The population mean of X is different to the population mean of Y
  - The alternative hypothesis will be: H₁: μ_x≠ μ_y
  - Look out for words such as change, different, not the same, etc
If you reject the null hypothesis then
- This suggests that the population mean of X is different to the population mean of Y
- You can not state which one is bigger as you were not testing for that
  - All you can conclude is that there is evidence that the means are not equal
  - To test whether a specific one is bigger you would need to use a one-tailed test

Worked example

In a school all students must study either French or Spanish as well as maths. 18 students in a maths class complete a test and their scores are recorded along with which language they study.

Studies French	61	82	77	80	99	69	75	71	81
Studies Spanish	74	79	83	66	95	79	82	81	85

The maths teacher wants to investigate whether the scores are different between the students studying each language. A t-test is to be performed at a 10% significance level.

Write down the null and alternative hypotheses.

4-7-4-ib-ai-sl-t-test-two-tail-a-we-solution