5.4.3 Further Applications of Integration

Negative Integrals

The area under a curve may appear fully or partially under the x-axis
- This occurs when the function $f (x)$ takes negative values within the boundaries of the area
The definite integrals used to find such areas
- will be negative if the area is fully under the $x$ -axis
- possibly negative if the area is partially under the $x$ -axis
  - this occurs if the negative area(s) is/are greater than the positive area(s), their sum will be negative

How do I find the area under a curve when the curve is fully under the x-axis?

STEP 1

Write the expression for the definite integral to find the area as usual

This may involve finding the lower and upper limits from a graph sketch or GDC and f(x) may need to be rewritten in an integrable form

STEP 2

The answer to the definite integral will be negative

Area must always be positive so take the modulus (absolute value) of it

e.g. If

I = - 36

then the area would be 36 (square units)

How do I find the area under a curve when all, or some, of the curve is below the x-axis?

Use the modulus function
- The modulus is also called the absolute value (Abs)
- Essentially the modulus function makes all function values positive
- Graphically, this means any negative areas are reflected in the $x$ -axis

5-4-3-ib-hl-ai-aa-extraaa-ai-run-fig1-neg-area

A GDC will recognise the modulus function
- look for a key or on-screen icon that says 'Abs' (absolute value)

$A = \int_{a}^{b} |y| d x$

- This is given in the formula booklet

STEP 1

If a diagram is not given, use a GDC to draw the graph of

y = f (x)

If not identifiable from the question, use the graph to find the limits

a

and

b

STEP 2

Write down the definite integral needed to find the required area

Remember to include the modulus ( | ... | ) symbols around the function

Use the GDC to evaluate it

Exam Tip

If no diagram is provided, quickly sketch one so that you can see where the curve is above and below the x - axis and split up your integrals accordingly
- You should use your GDC to do this

Worked example

The diagram below shows the graph of $y = f (x)$ where $f (x) = (x + 4) (x - 1) (x - 5)$ .

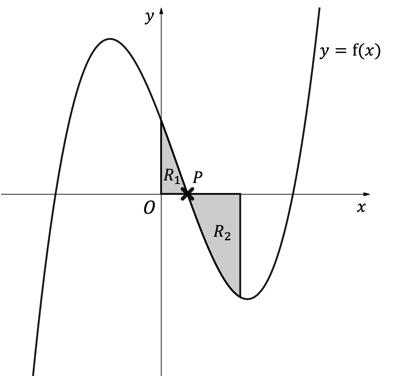
5-4-4-ib-sl-aa-only-we1-qu-img

The region $R_{1}$ is bounded by the curve $y = f (x)$ , the $x$ -axis and the $y$ -axis.

The region $R_{2}$ is bounded by the curve $y = f (x)$ , the x-axis and the line $x = 3$ .

Find the total area of the shaded regions,

R_{1}

and

R_{2}

QYldKmqS_5-4-3-ib-hl-ai-aa-extraaa-ai-we2-soltn

Area Between Curve & y-axis

What is meant by the area between a curve and the y-axis?

The area referred to is the region bounded by
- the graph of $y = f (x)$
- the $y$ -axis
- the horizontal line $y = a$
- the horizontal line $y = b$
The exact area can be found by evaluating a definite integral

How do I find the area between a curve and the y-axis?

Use the formula

$A = \int_{a}^{b} |x| d y$

- This is given in the formula booklet
- The function is normally given in the form $y = f (x)$
  - so will need rearranging into the form $x = g (y)$
- $a$ and $b$ may not be given directly as could involve the the $x$ -axis ( $y = 0$ ) and/or a root of $x = g (y)$
  - use a GDC to plot the curve and find roots as necessary

STEP 1

If a diagram is not given, use a GDC to draw the graph of $y = f (x)$
(or $x = g (y)$ if already in that form)
If not identifiable from the question, use the graph to find the limits $a$ and $b$

STEP 2

If needed, rearrange $y = f (x)$ into the form $x = g (y)$

STEP 3

Write down the definite integral needed to find the required area

Use a GDC to evaluate it

A GDC is likely to require the function written with ‘

x

’ as the variable (not ‘

y

’)

Remember to include the modulus ( | … | ) symbols around the function

Modulus may be called ‘Absolute value (Abs)’ on some GDCs

In trickier problems some (or all) of the area may be 'negative'
- this would be any area that is to the left of the $y$ -axis (negative $x$ values)
- $|x|$ makes such areas 'positive' by reflecting them in the $y$ -axis
  - a GDC will apply $|x|$ automatically as long as the modulus ( | ... | )symbols are included

Exam Tip

If no diagram is provided, quickly sketch one so that you can see where the curve is to the left and right of the y - axis and split up your integrals accordingly
- You should use your GDC to do this

Worked example

Find the area enclosed by the curve with equation $y = 2 + \sqrt{x + 4}$ , the $y$ -axis and the horizontal lines with equations $y = 3$ and $y = 6$ .

5-4-3-ib-hl-ai-aa-extraaa-ai-we1-soltn

Area Between a Curve and a Line

Areas whose boundaries include a curve and a (non-vertical) straight line can be found using integration
- For an area under a curve a definite integral will be needed
- For an area under a line the shape formed will be a trapezium or triangle
  - basic area formulae can be used rather than a definite integral
  - using a GDC, one method is not particularly trickier than the other
The total area required could be the sum or difference of the area under the curve and the area under the line

5-4-4-ib-sl-aa-only-curv-line-part-1

5-4-4-ib-sl-aa-only-curv-line-part-2

How do I find the area between a curve and a line?

STEP 1

If a diagram is not given, use a GDC to draw the graphs of the curve and line and identify the area to be found

STEP 2

Use a GDC to find the root(s) of the curve, the root of the line, and the x-coordinates of any intersections between the curve and the line.

STEP 3

Use the graph to determine whether areas will need adding or subtracting

Deduce the limits and thus the definite integral(s) to find the area(s) under the curve and the line
Use a GDC to calculate the area under the curve

\int_{a}^{b} |y| d x

Remember to include the modulus (|...|) symbols around the function

Use a GDC to calculate the area under the line - this could be another definite integral or

A = \frac{1}{2} b h

for a triangle or

A = \frac{1}{2} h (a + b)

for a trapezium

STEP 4

Add or subtract areas accordingly to obtain a final answer

Exam Tip

Add information to any diagram provided
Add axes intercepts, as well as intercepts between lines and curves
Mark and shade the area you’re trying to find
If no diagram is provided, use your GDC to graph one and if you have time copy the sketch into your working

Worked example

The region $R$ is bounded by the curve with equation $y = 10 x - x^{2} - 16$ and the line with equation $y = 8 - x$ .

$R$ lies entirely in the first quadrant.

Find the area of the region R.

5-4-3-ib-hl-ai-adapted-we3-soltn

Definite Integrals

What is a definite integral?

$\int_{a}^{b} f (x) d x = {[F (x)]}_{a}^{b} = F (b) - F (a)$

This is known as the Fundamental Theorem of Calculus
a and b are called limits
- a is the lower limit
- b is the upper limit
$f (x)$ is the integrand
$F (x)$ is an antiderivative of $f (x)$
The constant of integration (“+c”) is not needed in definite integration
- “+c” would appear alongside both F(a) and F(b)
- subtracting means the “+c”’s cancel

How do I find definite integrals analytically (manually)?

STEP 1

Give the integral a name to save having to rewrite the whole integral every time

If need be, rewrite the integral into an integrable form

$I = \int_{a}^{b} f (x) d x$

STEP 2

Integrate without applying the limits; you will not need “+c”
Notation: use square brackets [ ] with limits placed at the end bracket

STEP 3

Substitute the limits into the function and evaluate

Exam Tip

If a question does not state that you can use your GDC then you must show all of your working clearly, however it is always good practice to check you answer by using your GDC if you have it in the exam

Worked example

Show that

$\int_{2}^{4} 3 x (x^{2} - 2) d x = 144$

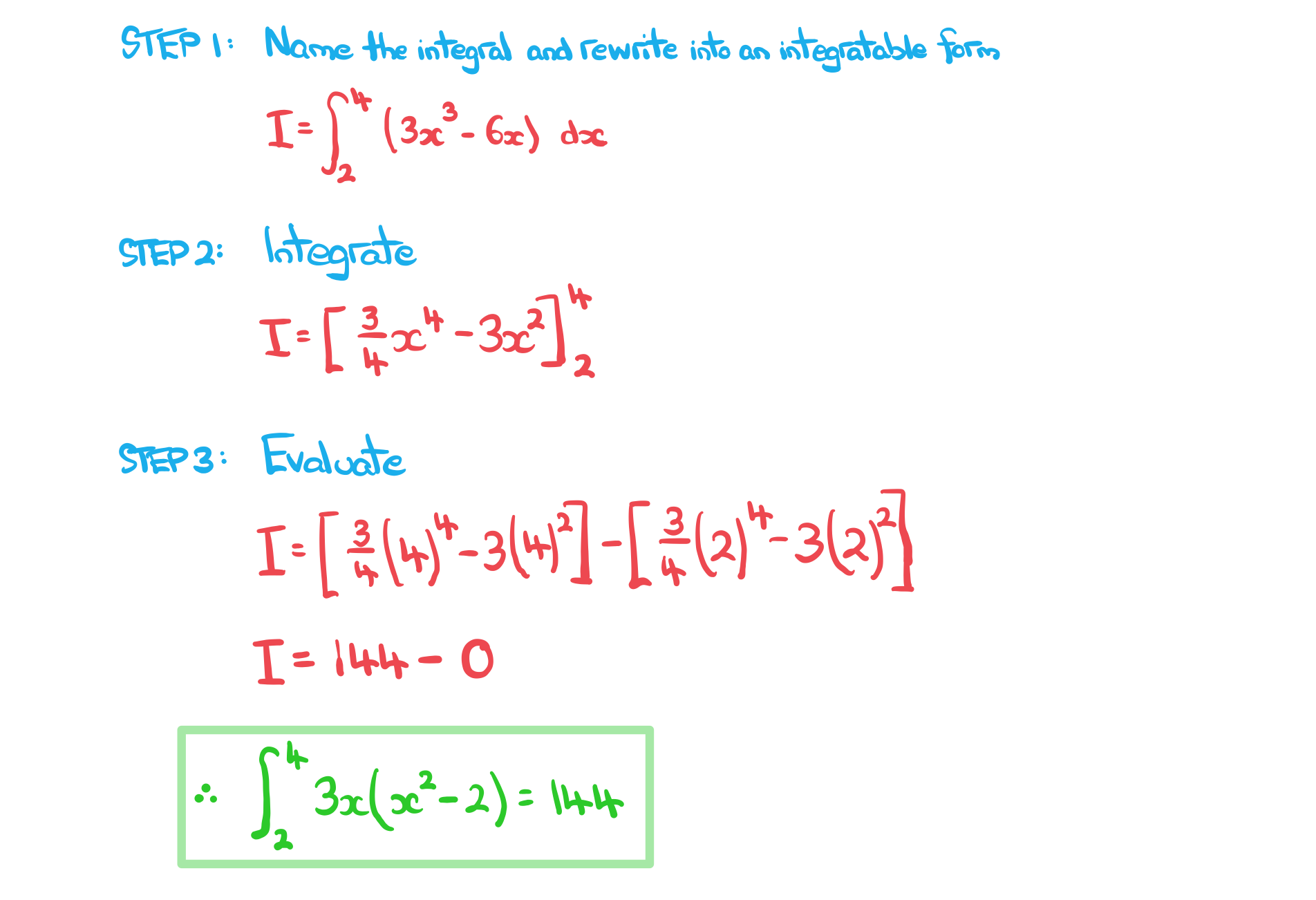
5-4-3-ib-sl-aa-only-we1-soltn-a

Use your GDC to evaluate

$\int_{0}^{1} 3 e^{x^{2} \sin x} d x$

giving your answer to three significant figures.

5-4-3-ib-sl-aa-only-we1-soltn-b

You've read 0 of your 0 free revision notes

Get unlimited access

to absolutely everything:

Downloadable PDFs
Unlimited Revision Notes
Topic Questions
Past Papers
Model Answers
Videos (Maths and Science)

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

DP IB Maths: AI HL

Revision Notes

5.4.3 Further Applications of Integration

Negative Integrals

How do I find the area under a curve when the curve is fully under the x-axis?

How do I find the area under a curve when all, or some, of the curve is below the x-axis?

Exam Tip

Worked example

Area Between Curve & y-axis

What is meant by the area between a curve and the y-axis?

How do I find the area between a curve and the y-axis?

Exam Tip

Worked example

Area Between a Curve and a Line

How do I find the area between a curve and a line?

Exam Tip

Worked example

Definite Integrals

What is a definite integral?

How do I find definite integrals analytically (manually)?

Exam Tip

Worked example

You've read 0 of your 0 free revision notes

Get unlimited access

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul